D-Cinema:
A Mathematical Model Of Prediction
Marco Del Mancino, Master’s degree in Marketing and
Market Research
What is D-Cinema? “The biggest technological
change in the field of the cinema since the advent of sound,” are the
words of John Fithian, President of the American exhibitors’s association
(NATO). The question circulating within the sector is becoming more a
matter of “when” this changeover will be considered operational. An answer
can be provided by using mathematical diffusion models, which have for
a long time been applied successfully in various sectors, with the aim
of foreseeing the spread of various phenomena: disease, information, products
or, as in this case, a type of technology.
Amongst the various models offered by sector literature, the epidemiological
and the pure imitation types would seem to offer interesting inspiration
(1) . This model hypothesises that, for the adoption of a
new type of technology (D-Cinema), what is relevant is mainly the information
that circulates amongst potential users through direct contact and/or
following the social-psychological pressure that an expanding market places
upon them. It is, in fact, quite clear that the more exhibitors opt for
D-Cinema, the less psychological opposition there will be from the remaining
potential users, thus reducing the legitimate fears that accompany the
transition from a well-known and reliable type of technology (35mm) to
a totally new one. We can thus speak of a sort of process of imitation:
a credible hypothesis on a business-to-business market where, at least
in the initial stages of the process, it is natural to imagine that adoptions
take place through the spread of information through direct contact with
other operators already using the new technology or, to a lesser extent,
through micro-social events, such as conferences and specialised events.
Of course this does not mean that the so-called external factor (ex. the
mass media, or the trade press) is completely irrelevant but that it probably
produces the same basic effect on all potential users who do, in fact,
acquire their information from the trade press itself; nevertheless it
is a secondary effect compared to that produced by direct, interpersonal
contact.
The sales history, or the number of “digital screens” throughout the world
from the introduction of the technology in 1999 up to 2005 confirms our
hypothesis. Observe the graph below: adoptions have actually followed
an almost perfectly exponential growth curve, supporting the hypothesis
of an “epidemiological” spread characterised, in this introductory phase,
by a very small number of innovators, growing more and more quickly year
by year.
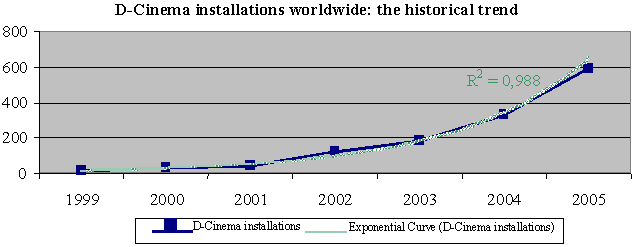
If then we accept the logic of “diffusion”,
the Mansfield model allows us to obtain a forecast of the spread of D-Cinema
in the world’s movie theatres using the values of the potential market
(the number of commercial theatres in operation today,
assumed to be constant) and the history of adoptions (MEDIA Salles, Screen
Digest, MPAA data). The results of the model are illustrated as follows.
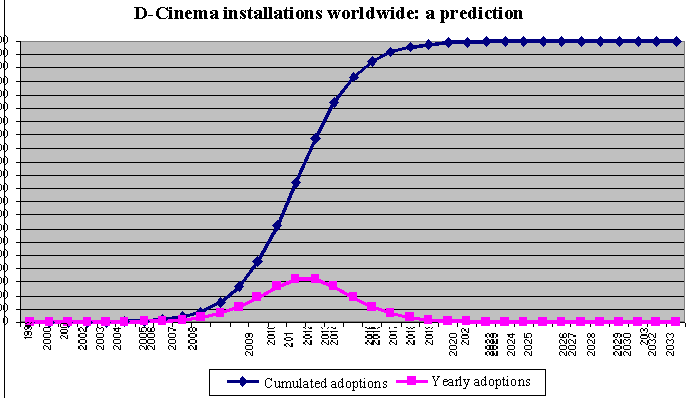
Our model forecasts that although 99% of
the potential market will not be fully covered until 2020, the peak will
already be reached in 2014 (with over 16 thousand new installations),
a year in which 35mm technology should be outstripped, with D-Cinema in
operation on around 65% of the world’s cinema screens.
This forecast foresees a process of adoption that is considerably slower
compared to some hypotheses, that predict about 80,000 projectors in 2009,
yet certainly does not confirm the more pessimistic vision circulating
in the sector which contemplates the two types of technology co-existing
for a long period, something that would happen, on the other hand, if
problems due to an “excess of inertia” (the “Shall-I-go-first-no-after-you”
syndrome) failed to be solved, or the definition of standards, typical
in the process of any technological changeover.
The existence of different and clashing forecasts reflects the difficulty
of anticipating developments in processes of an exponential nature, especially
if a solid mathematical model is lacking for reference. Typically, these
phenomena tend to be underestimated in their very early stages and then
over-estimated when the exponential growth becomes more evident. Our model,
instead, although perfectly compatible with an initial phase of exponential
increase, does not assume constant growth: after reaching its peak, the
number of yearly adoptions gradually begins to fall. The most evident
effect of this mechanism is the extremely slow process of reaching the
saturation point: the adoption of D-cinema by the remaining 1% of the
potential adopters (the “laggards”) of the market seems to take over 10
years, where conditions remain the same. This is a defect typical of models
(and processes) that do not foresee external sources of communication.
It goes without saying that the reality is certainly (and by definition)
more complex than the model suggested and, like any forecast, must be
taken with a grain of salt. In any case we believe that this analysis
can make a useful contribution to the debate on D-cinema. The model presented
is not, in fact, a crystal ball for foreseeing the future, but makes it
possible to indicate, on the basis of figures and strict mathematical
logic, what will happen if the market continues to grow according to the
“epidemiological” patterns seen up to the present – a hypothesis that
naturally excludes outside events (although probable), such as a decision
by the Hollywood majors to systematically adopt the new technology, which
would obviously speed up its spread.
The accuracy of the forecasts offered by the model could be improved by
introducing some more complex elements suggested by specialised literature,
such as: reduction in the price of projectors and the introduction of
outside communication, for example by the mass media, contrasting profiles
amongst potential users. It is nonetheless useful to note that from the
qualitative point of view, all these elements would produce effects pointing
in only one direction: a more or less considerable acceleration in market
saturation time.
(1)
Regards the “Mansfield Model”, see Mansfield 1961, Mahajan 1993 and Manfredi
1996.